Let Us YOU Solve Physics JEE (MAIN) 2017 Physics Paper
We continue with Physics questions from JEE (Main) 2017, Paper-1. All are MCQs with single correct option. Ticking the correct option fetches full 4 marks; ticking incorrect option or multiple options fetches -1 mark. So never rely on wild guesses! Hint on every question is followed by a video solution, to be consulted strictly at the end of your own solution. The video lectures referred in the discussion can be accessed @ PhysicsAcademyOnline.com.
One more thing. Our freewheeling discussion on every question will obviously consume some time. But remember! While in examination hall, you should ideally take two minutes to solve a question, and then move on to the next question. Time is, indeed, a decisive factor in competitive exams.
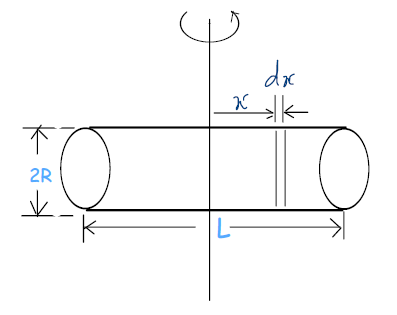
Question 05: The moment of inertia of a uniform cylinder of length L and radius R about its perpendicular bisector is I. What is the ratio, L/R, such that the moment of inertia is minimum?:
(1) √(3/2) (2) √3/2 (3) 1 (4) 3/√2
Frankly speaking, this question is quite difficult compared to the others dealt so far at JEE (Mains) level. However, not only shall we guide you at every step to solve the question, we shall give you some practical advice as well.
First, the time factor. The solution is bound to take some precious time. So just like a good batsman ducks a bouncer on occasions, you might do well to skip the question as it comes and return to solve it at the end, time permitting. It’s not wise to repent later that one question’s solution took away the time for three other questions!
There is no ready-made formula for moment of inertia, I, of a cylinder about its perpendicular bisector. To calculate that, first learn the calculus-based technique from the following lecture: Chapter Name – Mechanics; Category – Basic; Topic Name – Rotational Mechanics; Video Name – Moment of Inertia, and Its Calculation for Various Bodies.
Let us chip in with a diagram. Take an infinitesimal disc of thickness dx at distance x from the perpendicular bisector. What is its moment of inertia, dI, about the bisector? Two more lectures will be useful: Chapter Name – Mechanics; Category – Basic; Topic Name – Rotational Mechanics; Video Names – “Two Important Theorems on Moment of Inertia” & “Applications of Parallel and Perpendicular Axes Theorems”.
Integrate dI over the length of cylinder to find I. Express it in terms of a single variable, L. Under what condition is I the minimum? Recommended a typical problem on Maxima and Minima from: Chapter Name – Mechanics; Category – Advanced; Topic Name – Vectors; Video Name – Advanced-Level Problems on Vectors I (problem 1).
Go ahead and pick your choice. Lest it leaves any doubt in your mind, confirm from the detailed video solution below.
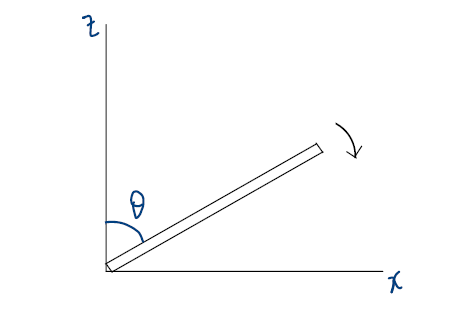
Question 06: A slender uniform rod of mass M and length L is pivoted at one end, so that it can rotate in a vertical plane (see figure) . There is negligible friction at the pivot. The free end is held vertically above the pivot, and then released. The angular acceleration of the rod when it makes an angle θ with the vertical is:
(1) 3g sinθ /2L (2) 2g sinθ /3L (3) 3g cosθ /2L (4) 2g cosθ /3L
What is the equation of motion of a rod rotating about any axis? Watch the lecture: Chapter Name – Mechanics; Category – Basic; Topic Name – Rotational Mechanics; Video Name – Equation of Rotational Motion of a Rigid Body.
What is/are the force(s) acting on the rod after release? What is the net torque about the pivot at angular position q from the vertical? Study from here: Chapter Name – Mechanics; Category – Basic; Topic Name – Rotational Mechanics; Video Name – Torque of a Force Acting on a Particle.
What is the moment of inertia of the rod about (the axis of rotation through) the pivot? If you need to look again: Chapter Name – Mechanics; Category – Basic; Topic Name – Rotational Mechanics; Video Name – Applications of Parallel and Perpendicular Axes Theorems.
Little work is left after this.