
Test
In class XI physics course, the topic of "Physical Quantities and Their Measurements" is a useful introduction. A physical quantity is measured in terms of a small part of it. The small part is conventionally adopted as a unit of measurement of the quantity. It is helpful to first establish the units of a few quantities which are called base quantities or fundamental quantities. The corresponding units are called base units or fundamental units. The units of the remaining physical quantities are expressed in terms of these base units. These quantities are called derived quantities, and their units are called derived units. The set of base and derived units is called a system of units.
In 1960, an international committee called CGPM adopted the International System of Units or SI which has been supplemented and refined ever since. The group of SI units consists of seven base units and two supplementary units.
The concept of order of magnitude is often very helpful to compare the magnitudes of two or more physical quantities of the same type. At first the absolute value of a given quantity is written in the form
x × 10y where 1≤ x< 10 and y is a positive or negative integer. Next, the number is rounded off according to specific guidelines. The power of 10 in the final representation is called the order of magnitude of the quantity. For instance, the mass of the earth is
about 5.98 × 1024 kg and the mass of an electron is about 9.11 × 10-31 kg.
By the above rules, the mass of the earth is of the order of 1025kg and the mass of an electron is of
the order of 10-30 kg .
Therefore, the mass of the earth is 25 - (-30) = 55 orders of magnitude larger than the mass of an electron.
The word dimension in physics means the physical nature of the quantity.
The dimensions of a quantity should not be confused with its units. To illustrate the point,
the distance between two places can be measured in different units such as metre, centimetre, foot etc. But the dimension of
distance is always the same, which is "length". The usual practice is to use square brackets, [ ], to denote the dimensions of a
physical quantity. Thus, the dimension of distance is [L] , the dimension of mass is [M],
the dimensions of velocity and force are [LT-1] and [MLT-2] respectively.
Any equation that relate several physical quantities must be homogenous from the dimensional point of view. If an equation is of the form A = B + C, then A, B and C must represent the same physical quantity with the same dimensions. This property is known as the principle of homogeneity of dimensions. To illustrate the point, let us take an important equation from Kinematics:
x - x0 = ut + ½ at2
Here (x-x0) is the distance travelled by a particle along a straight line in time t, u is the initial velocity of
the particle and a is the constant acceleration with which the particle is moving.
The dimension of (x - x0) is [L], the dimension of ut is [LT-1][T] = [L],
and the dimension of at2 is [LT-2][T2] = [L]. Therefore,
the dimensional form of the equation can be written as:
[L] = [L] + [L]
which demonstrates that the equation is dimensionally homogenous.
The method of dimensional analysis has many uses:
Each one of them will be discussed with examples in due course.
We can never measure a physical quantity with absolute precision. The degree of accuracy of any measurement depends on the smallest scale division of the measuring instrument. This is known as the least count of the instrument. The least count of an ordinary metre scale is 0.1 cm or 1 mm. When we use it to measure the length of a certain steel rod, suppose the reading falls somewhere between 24.6 cm and 24.7 cm marks. So we divide the space between the two marks mentally in 10 equal parts and guess how many of these parts are the from the 24.6 cm mark to the end of the rod. Let this number be 3. Accordingly, the length of the rod is taken as 24.63 cm. So we see here that the first three digits counted from the left, i.e. 2, 4 and 6 are certain but the fourth digit 3 is uncertain. The significant figures of any measurement are the digits which are reasonably reliable. By convention, they consist of all the certain digits and only one uncertain digit. Thus, a metre scale can read up to four significant figures (2, 4, 6 and 3 in our example).
Certain points should be kept in mind while counting significant figures in a number. Certain rules are to be followed in counting significant figures in the answer of algebraic operations such as multiplication, division, addition and subtraction. They will be discussed in due course.
Any experiment involves a series of measurements. Several errors may occur during these measurements. The errors in measurement can be classified into two basic types: systematic error and random error.
Often we wish to find the value of a quantity Z that involves the measurement of two other quantities X and Y.
The combined error in the value of Z depends not only on the errors in the values of X and Y, but also on the nature of
dependence of Z on X and Y. There are specific formulas which we can develop to calculate the
combination of errors for various cases such as
Z = X + Y, Z = X - Y, Z = XY, Z = X / Y, Z = Xn,
or a more general type U = k Xa Yb / Zc.
The physical quantities which we encounter in our daily lives may be broadly divided into two groups: scalars and vectors. A quantity which is completely specified by a number with an appropriate unit is called a scalar. It has only magnitude but no direction. Examples are mass, distance, time, speed, work, temperature, volume etc. A quantity which is completely specified by a number with an appropriate unit and a direction is called a vector. Thus, it has both magnitude and direction. Some examples of vectors are displacement, velocity, acceleration, force, momentum, torque, gravitational field etc.
Vector quantities follow the rules of vector algebra, which are different from the rules of arithmetic. This is an important criterion for checking whether a quantity is vector or not, as we shall see when we study Rotational Mechanics.
The graphical representation of a vector is a straight line with an arrowhead on one tip. The length of the line segment represents the magnitude of the vector on a convenient scale; the arrowhead gives the direction of the vector.
Three or more vectors which are in the same plane or are parallel to the same plane are called coplanar vectors. Equal vectors are those which have the same magnitude, same or parallel lines of support, and the same sense. The negative of a vector is the one whose magnitude is equal to that of the given vector, but the direction is opposite. A zero vector or null vector is the one which has zero magnitude and no specific direction. The position vector of a point represents the position of the point with respect to the origin of any coordinate system. The unit vector is obtained by dividing a vector by its magnitude. The magnitude of a unit vector is 1 (no unit), and its direction is the same as that of the original vector. As an example, if a force vector is 5 N directed southwards, the corresponding unit vector will be 1 due south.
The rules of addition of vectors are more complicated than those of arithmetic addition. The addition gives a resultant vector which produces the same effect as the combining vectors produce together. Two vectors can be added, both graphically and analytically, by the triangle law of vector addition or parallelogram law of vector addition. Several vectors can be added graphically by the polygon law of vector addition. For a more accurate addition of several vectors, analytically, we make use of addition of vectors by resolution method.
The subtraction of vectors follows similar approach as addition of vectors, with an important difference. The subtraction of one vector from another is defined as the addition of the negative of the vector to be subtracted. If P and Q are two vectors with the same unit then:
P - Q = P + (- Q)
The resolution of a vector is the process of determining a set of vectors which produce together the same effect as the original vector does alone. Each vector in the set is known as a component vector of the original vector. Thus, the process of resolution is opposite to the process of vector addition. Among many possibilities of resolution, the most useful ones are the resolution of a vector on a plane along two mutually perpendicular x- and y-axes AND the resolution of a vector in space along three mutually perpendicular x-, y- and z-axes.
Like addition and subtraction, the multiplication of vectors follows a set of rules different from those of arithmetic multiplication. The vectors to be multiplied need not have the same unit. There are two types of product known as the scalar product or dot product AND vector product or cross product.
The scalar product of two vectors is a scalar quantity equal to the product of the magnitudes of the given vectors and the cosine of the angle between them. The physical quantity "work" is the scalar product of force vector and displacement vector.
The vector product of two vectors is a vector quantity whose magnitude is equal to the product of their individual magnitudes and the sine of the smaller angle between them. The direction of the vector product is perpendicular to the plane containing the given vectors and its sense is determined by the right-hand corkscrew rule or the right-hand thumb rule, discussed in due course. The physical quantity "torque"is the vector product of displacement vector and force vector.
Historically, the term mechanics was first used by Sir Isaac Newton to mean the science of machines and the art of making them. Today we use the word to mean the branch of science that describes and predicts the conditions of rest or motion under the effect of a set of forces. Mechanics can be divided into two parts: dynamics and statics. Dynamics is the study of motion of a body under one or more forces. Statics is the study of the condition of rest of a body under a number of forces. Dynamics is further divided into kinematics and kinetics. Kinematics is that part of dynamics which deals with motion ignoring the forces that cause it or the properties of the body in motion. Presently, we shall deal with kinematics here. Kinetics is that part which relates the motion of a body to its mass and the causal force(s). Newton's laws of motion , which are a fundamental part of kinetics, will be dealt next.
A body is a portion of matter which extends over a certain region of space and has a definite shape and size. But the study of motion of a body can be made simpler by ignoring its size and shape, and, assuming that the whole mass of the body is concentrated at a point occupying a definite position in space. In that event, we refer to the body as a particle. The particulate view of body is valid in many practical situations. The size of the earth and the sun are huge in absolute terms, but both are much smaller than the distance between them. Therefore, when we study the motion of the earth round the sun, we can treat both of them as particles!
When we observe a nearby object on the earth's surface, we intuitively determine whether it is at rest or in motion with respect to the ground. But considering the fact that the ground itself is in motion (earth rotates about its own axis and, simultaneously, revolves round the sun), the difference between rest and motion is not as clear-cut as one may think. The early scientists who searched for an absolutely fixed body met with little success. It was Albert Einstein who finally suggested that there is nothing called absolute rest or absolute motion. Rest and motion are purely relative concepts, and the significant thing is whether the body under investigation is at rest or in motion with respect to its local surroundings. These local surroundings are known as the frame of reference.
The frame of reference is usually pictured in terms of a three-dimensional rectangular coordinate system, often called cartesian coordinate system, consisting of three mutually perpendicular axes intersecting at a point. The axes are designated as x-, y- and z-axes; the point of intersection, marked by the letter O, is known as the origin of the system.
The motion of rigid bodies can be of two types: translational motion and rotational motion. When a rigid body performs translational motion, all particles constituting the body travel with the same velocity and acceleration at any given instant. Hence the paths followed by them have the same length and are parallel to each other. If these paths are straight lines, we say the body is in rectilinear motion (that is, motion in a straight line). Example: motion of a car along a flat, straight, narrow road. If the paths of the particles are curved, the body is said to be in curvilinear motion. An interesting example is the motion of a wooden horse on a merry-go-round.
When a rigid body performs rotational motion, the particles of the body located at different radial distances from the axis of rotation travel with different velocities and accelerations at any given instant. Hence the paths followed by them have different lengths. Example: motion of a fan blade or a spinning wheel.
The motions we see around us are often a combination of translation and rotation. The rolling motion of a sphere on the floor is one such example.
Presently, we shall study translational motion in one dimension and in two dimensions. The study of pure rotational motion and rolling motion will be done later within Mechanics.
Here are some terms associated with translational motion. Suppose a particle which is at position P1 at time t1 moves to a new position P2 at time t2 following a curved path P1P3P2 .
The length of the actual path gives the distance travelled by the particle. Distance is a scalar quantity without direction. The displacement, on the other hand, is given by the straight line P1P2 which joins the initial and final positions of the particle. Displacement is a vector quantity. The magnitude of displacement is the length of the straight line P1P2 , and its direction is from P1 to P2 . Both distance and displacement have the same dimension of length, [L], and have the same SI unit metre (m).
The speed of a moving particle is the distance travelled by it in unit time. Speed is a scalar quantity. The velocity of a particle is its displacement per unit time. Velocity is a vector quantity. Both speed and velocity have the same dimensions, [LT -1] , and have the same SI unit metre per second (m/s).
The acceleration of a particle is the rate of change in velocity with time. The change in velocity may be due to a change in its magnitude, direction or both. Like displacement and velocity, acceleration is a vector quantity. The dimensions of acceleration are [LT-2], and its SI unit is metre per second square (m/s2). Negative acceleration is known as deceleration or retardation.
Graphical analysis of rectilinear motion, as the name suggests, is the visualisation of a particle's straight-line motion with the help of a graph. Two commonly plotted graphs are position versus time graph and velocity versus time graph.
The simplest example of accelerated motion is rectilinear motion with constant acceleration. It is possible to develop a useful set of kinematic equations either by graphical method or by the method of calculus (integration). These equations involve quantities such as displacement, time, initial and final velocities, and acceleration. The vertical motion of a freely falling body under gravity is a case of rectilinear motion with constant acceleration. A more complicated case is rectilinear motion with variable acceleration. When a body moves back and forth about a point in simple harmonic motion (a special case of periodic motion), its acceleration varies as a function of its displacement. Problems of this type will also be dealt with in due course.
The kinematic equations developed for rectilinear motion can be suitably modified to analyse motion in a plane, that is, motion in two dimensions. If a particle is thrown obliquely in air near the earth's surface, it follows a curved path that lies in a vertical plane. The particle is called a projectile, and the path followed by it is called a trajectory. A bullet fired from a gun or a ball hit by a cricket bat is an example of a projectile. Assuming acceleration due to gravity, g, remains constant throughout and air resistance is negligible, projectile motion is an example of motion in a plane with constant acceleration.
Other examples of two-dimensional motion are circular motion and motion of a boat in a river.
The relative velocity of a body with respect to another body is defined as the rate of change of position of the first body as observed by the second body. It is given by the vector difference between their absolute velocities. Similarly, the relative acceleration of a body with respect to another body is defined as the rate of change of velocity of the first body as observed by the second body. This is given by the vector difference between their absolute accelerations.
Kinetics is the study of how the motion of a body is related to its mass and the force(s) acting on it. The force represents the interaction of a body with its environment. The mass of a body is a measure of its inertia, which is the tendency to resist acceleration under a force. Newton's laws of motion are fundamental to the study of kinetics.
Newton's three laws of motion were first published in his celebrated work
Mathematical Principles of Natural Philosophy in the year 1687. We shall touch upon each of them.
Newton's first law of motion: A body at rest continues to remain at rest and a body in motion continues in motion with a constant velocity unless it is compelled by a net external force to change that state.
The statement of the first law provides two important concepts:
Newton's first law is often called the law of inertia. Any frame of reference in which Newton's first law is valid is called an inertial frame of reference. Qualitatively, a force is defined as an external agent which, when applied to a body, changes its state of rest or of motion with a constant velocity.
Newton's second law of motion: The rate of change in momentum of a body is proportional to the net external force that acts on the body and it takes place in the direction in which the force acts. The statement of the second law provides two more concepts:
Momentum is given by the product of the mass and velocity of a particle. Since mass is a scalar and velocity is a vector, momentum is a vector quantity which has the same direction as velocity. The dimensions of momentum of are [MLT-1], and its SI unit is kilogram metre per second (kg-m/s).
Quantitatively, force is given by the product of mass and acceleration. Since mass is a scalar and acceleration is a vector, force is a vector quantity which has the same direction as acceleration. The mathematical statement of Newton's second law is:
F = ma
This very important equation is called equation of motion. The dimensions of force are [MLT-2], and its SI unit is newton (N).
Newton's third law of motion: To every action there is always an equal and opposite reaction. In all cases, the action and reaction forces act on different bodies.
Whenever a particle 1 exerts a force of action, F21, on another particle 2, the latter also exerts a force of reaction, F12, on the former. These two forces are equal in magnitude and opposite in direction. They act along the same line joining the two particles. Therefore, we can write:
F12 = -F21
The above relationship is mutually reciprocal. That is, either of the two forces can be thought to be the action force and the other, the reaction force. Another important aspect of the third law is, even though forces always occur in pairs, they always act on two different bodies and do not cancel each other. If they were to act on the same body, the net force on the body would be zero and it could never have an acceleration!
Newton's second and third laws can be applied to explain a variety of events around us. But the first and foremost step towards that is to learn how to draw free body diagrams. Every time you want to write the equations of motion of a body, it is advised that you isolate the body from its surroundings, identify all the forces acting on it and show them clearly in a separate diagram. No need to show the bodies which exert the forces. The forces of reaction, which are exerted by the body under investigation, do not appear in the diagram. A force diagram of this type is known as a free body diagram. A correct free body diagram usually means correct equations of motion and a straightforward solution to the problem.
Among the many applications of Newton's second and third laws, problems on pulleys and wedges are of particular interest. The type of motion in which the velocities or accelerations of two or more particles depend on each other is known as constrained motion. When we analyse a constrained motion by applying Newton's laws, we must take into account additional conditions imposed on such a motion. This conditions are known as constraints. We shall discuss constrained motion of two types of system: pulley-block system and wedge-block system.
Any frame of reference, which accelerates with respect to an inertial frame of reference, is called a non-inertial frame of reference. Newton's laws are not valid in such a frame of reference. The net force acting on a particle in a non-inertial frame is made up of two parts: a real force and a fictitious force. The fictitious force, which has no material source, is called pseudo force and given by - ma0 , where m is the mass of the particle and a0 is the acceleration vector of the non-inertial frame with respect to the inertial frame. The pseudo force(s) do not exist when the motion is observed from an inertial frame.
We often simplify a problem by assuming that the motion of bodies takes place on "frictionless" surfaces. But in real world, all motions happening around us are affected by the force of friction. Therefore, a realistic approach to any mechanical problem requires that we identify the frictional forces acting on the system and include them in the respective equations of motion. Suppose a block 1 is placed on top of another block 2.
As long as the blocks are at rest and there is no attempt to produce a relative motion between them, the contact forces acting in a pair between the blocks are purely normal forces and directed perpendicular to the surface separating the blocks. But if a driving force F is applied to block 1 in an attempt to drag it to the right along the surface of block 2, the contact forces between the blocks act at an oblique angle to the surface of separation.
The components of contact forces perpendicular to the surface are the normal forces N and - N. The components of contact forces parallel to the surface are the frictional forces f and - f . By Newton's third law, these frictional forces always act in an action-reaction pair. Their directions are such that they resist any real or impending relative motion between the two blocks. In our case, since the driving force F is applied to the right, the frictional force on block 1 acts to the left and the frictional force on block 2 acts to the right.
The resistance to the relative motion between two solid bodies is known as solid friction, or simply friction. The resistance to the relative motion between a solid body and a fluid is known as fluid friction, or more commonly as drag force. The relative motion between two solid bodies can be produced in two different ways.
They can either slide over one another or they can roll over one another. Accordingly, solid friction can be classified into two types: sliding friction and rolling friction. And again, the friction that exists when the bodies are about to slide over one another is not the same as the friction that exists when the bodies are actually sliding over one another. The first type is called static friction, and the second type is called kinetic friction.
Consider a block of mass m resting on a rough, horizontal surface. A driving force F is applied rightwards to the block. As the magnitude of F is increased slowly, the force of static friction fs acting leftwards on the block also increases equally in magnitude to keep the block at rest. When the block is just about to move to the right, the force of static friction attains its maximum value which is called the force of limiting friction.
According to the laws of static friction, force of limiting friction is directly proportional to the magnitude of the normal force between the two surfaces. In other words, the ratio of force of limiting friction and normal force is a constant known as coefficient of static friction. Once the block begins to move, the force of kinetic friction fk comes into play, which is usually smaller than the force of limiting friction. By the laws of kinetic friction, force of kinetic friction is also directly proportional to the magnitude of normal force. The corresponding ratio of force of kinetic friction to normal force is a constant called coefficient of kinetic friction. Generally, the first coefficient is greater than the second for a given pair of surfaces.
It will be useful to introduce few more terms. Suppose a block rests on a rough plane inclined at a small angle to the horizontal. The angle of inclination is gradually increased until, at a certain point, the block is just about to slide down the incline. The corresponding angle of inclination of the plane is known as angle of repose.
The angle of friction between a given pair of surfaces is the angle between the total contact force and the normal force at the instant when one surface is just about to slide over another.
If the driving force acting on a block is slowly rotated through 360° keeping it parallel to the surface of the floor, the total contact force acting on the block remains within an imaginary inverted right circular cone, as long as the block is at rest. This cone is known as cone of friction.
The study of circular motion is not only important in itself, but also an essential pre-condition for the study of rotational motion later under Mechanics. We start with the definitions of the angular quantities in circular motion.
Suppose a particle is moving in a circle in the counterclockwise direction. The centre of the circle coincides with the origin O of the coordinate system Oxy. The initial position of the particle is P1 at time t1. The final position of the particle is P2 at a later time t2 . The angular displacement of the particle is equal to the angle swept by its position vector as it moves from OP1 to OP2 . Angular displacement is a pure number without dimensions. However, it is customary to express it in an artificial supplementary SI unit called radian (rad).
The angular velocity of the particle is its angular displacement per unit time. In uniform circular motion, the angular velocity has the same value at every instant. In nonuniform circular motion, the angular velocity keeps changing from one instant to another. The dimension of angular velocity is [T-1] ; its unit is radian per second (rad/s) or simply per second ( /s) since radian is a dimensionless unit. The time taken by a particle to complete one revolution is known as its time period. The number of revolutions completed by the particle per second is called its frequency.
In the case of nonuniform circular motion, the angular acceleration of a particle is the rate of change in angular velocity with time.The dimension of angular acceleration is [T-2] ; its unit is radian per second square (rad /s2), or just per second square ( /s2).
It is useful to note the relations between linear and angular quantities. A particle, moving in a circle of radius r, changes its position from P1 at time t1 to P2 at time t2 . The distance travelled by the particle is the length of the arc P1P2 . This distance is equal to the product of its angular displacement and radius of the circle. Similarly, the linear speed of a particle moving in a circle at any instant is the product of its angular speed and circle's radius.
The linear acceleration of a particle in circular motion has two components: tangential and radial. The tangential acceleration at any instant is the product of its angular acceleration and circle's radius. The radial acceleration, or centripetal acceleration as it is more commonly called, is the product of angular speed squared and circle radius.
Circular motion of a particle with constant angular acceleration is analogous to motion in a straight line with constant linear acceleration. Therefore, it is possible to develop a set of kinematic equations of circular motion in the same way as we did it for rectilinear motion. These equations involve quantities such as angular displacement, initial and final angular velocities, and angular acceleration.
When a particle performs uniform circular motion, its angular acceleration is zero, which means its tangential acceleration is also zero. The only acceleration present is the centripetal acceleration directed radially towards the centre of the circle. According to Newton's second law, the particle experiences a net external force – directed radially inwards – of magnitude given by the product of the mass of the particle and its centripetal acceleration. This force is known as centripetal force. An example of centripetal force is the gravitational force exerted by the sun on the earth which makes the latter revolve round the sun. In a rotating non-inertial frame of reference, a particle experiences a pseudo force directed radially outwards. This pseudo force is known as centrifugal force.
When a particle performs nonuniform circular motion, its tangential acceleration and centripetal acceleration are both non-zero quantities. Therefore, by Newton's second law, the net external force acting on the particle is the resultant of a tangential force and a centripetal force. A sphere moving in a vertical circle at the end of a light string constitutes a case of nonuniform circular motion.
The work done by a force on a particle is defined as the product of the component of the force in the direction of the displacement and the magnitude of the displacement. Suppose a constant force F acts on a block to produce a displacement s in it. The angle contained between the vectors F and s is θ . Then the work done by the force is:
W = Fs cos θ
Work is the scalar product of force and displacement vectors, which means work itself is a scalar and has no direction. If the angle between F and s is an acute angle (< 90°), work is positive. If the angle between F and s is an obtuse angle (> 90°), work is negative. If the angle between F and s is 90° , work done is zero. When a block moves on a horizontal floor, the force of gravity exerted by the earth and the normal force exerted by the floor do not do any work on the block because these forces act at right angles to the motion of the block. The dimensions of work are [ML2T-2], and its SI unit is joule (J).
To calculate the work done by a varying force, we need a more rigorous, calculus-based approach. Let us consider the case of a block attached to a spring. Suppose one end of a spring is attached to a fixed wall and the other end is attached to a block resting on a horizontal, frictionless floor. Initially, the spring is at its natural length. Now if an external force is applied to the block to move it slowly without acceleration further away from the wall, the spring stretches and exerts a variable restoring force opposite to the block's motion. The magnitude of this spring force is directly proportional to the displacement of the block.
The constant of proportionality is known as the force constant of the spring. If the spring is stretched to take the block from initial position x = 0 to final position x = x, it can be shown by integration that the work done by the external force is:
Wext= 1/2 kx2
The corresponding work done by the spring force is:
Wspr= -1/2 kx2
Here k is the force constant of the spring. Notice that the external force does positive work because it has the same direction as the block's displacement. The spring force does negative work (of the same absolute value) because it is directed opposite to the block's displacement.
The energy of a body can be loosely defined as its capacity of doing work, measured by the total amount of work the body can do. Energy can be of different types, e.g. mechanical, thermal, light, electrical, magnetic, sound, chemical and nuclear. In classical mechanics, we shall mostly deal with mechanical energy which is further classified into two types: kinetic energy associated with the motion of a body, and potential energy associated with the configuration of a system such as gravitational, elastic and electrical potential energy. All types of energy have the same dimensions and units as those of work.
The kinetic energy K of a particle of mass m moving with speed v is defined as:
K= 1/2 MV2
This is a scalar quantity which is always positive. According to the work-energy theorem, the net work done on a particle is equal to the change in its kinetic energy. In mathematical terms:
Wnet = 1/2 mv22 - 1/2 mv12 = K2 - K1 = ΔK
where v1 and v2 are the initial and final speeds, K1 and K2 are the initial and final kinetic energies, Δ K is the change in kinetic energy of the particle.
The power supplied by a force is defined as the rate at which the force does work. It is the scalar product of force and velocity vectors. That is:
P = F.v = Fv cos θ
where θ is the angle contained between F and v. The dimensions of power are [ML2T-3], and its SI unit is watt (W).
The potential energy of a system is the energy possessed by it by virtue of its configuration. It is measured by the work the system can do if it returns from its present configuration to some standard configuration usually associated with zero potential energy.
Forces in nature can be divided into two groups: conservative force and non-conservative force. A force is conservative if the total work done by it on a particle moving in a closed path is zero. In other words, the work done by a conservative force on a particle is independent of the path it takes to move from one point to another. Examples: force of gravity, spring force.
The energy diagram is the graph that shows the variation in the potential energy U(x) of a system with the displacement x of a particle forming part of the system. Energy diagram helps us to determine whether a body is in stable equilibrium, unstable equilibrium or neutral equilibrium.
According to the principle of conservation of mechanical energy, the total mechanical energy of an isolated system of particles which interact only through conservative forces is constant. If K1 , U1 are the initial values and K2 , U2 are the final values of the kinetic and potential energies of the system then:
K1 + U1 = K2 + U2
The principle can be applied to solve a host of mechanical problems. The method is often referred to as the energy method of solving a problem. It is usually more elegant and easier than force-based dynamical method of solving a problem.
Another conservation principle with broader scope is the principle of conservation of energy. It states that energy can neither be created nor destroyed. It may be transformed from one form to another, but the total energy of an isolated system is always constant. From a universal point of view, the total energy of the universe is constant.
Any discussion on energy conservation remains incomplete without reference to Einstein's famous formula on equivalence of mass and energy:
E0 = m0 c2
In this expression, m0 is the rest mass of a particle, E0 is the rest energy which is energy equivalent of m0 , and c is the speed of light in vacuum.
As the title suggests, the topic can be broadly divided into three sections. In the first section, we define the impulse of a force and state the impulse-momentum theorem. In the second section, we develop the principle of conservation of linear momentum and apply that to study collision between two bodies. In the third and final section, we define centre of mass of a system of particles and determine its position for various cases.
The impulse of a constant force is given by the product of the force and its duration. If the force is F and its duration is ∆ t , the impulse is given by:
I = F ∆ t
Impulse is a vector; its direction is the same as that of of the force. The dimensions of impulse are [MLT-1], and its SI unit is kilogram metre per second (kg-m/s).
Suppose the momentum of a particle changes from p1 at time t1 to p2 at time t2 under a force F applied over the interval ∆ t = t2 - t1.
It can be shown from Newton's second law of motion that:
I = F ∆ t = p2 - p1 = ∆ p
In words, the impulse of a force acting on a particle is equal to the change in linear momentum of the particle. This is the statement of the impulse-momentum theorem. If the force varies in magnitude and/or direction with time, the deduction becomes a little complicated. However, the impulse-momentum theorem holds. This last result shows that, for a given change in momentum of a particle, the force is inversely proportional to its duration. We should mention impulsive force in this context. Blows, collisions and explosions involve this type of force whose magnitude is very large and duration is extremely small.
Impulse-momentum theorem can be successfully applied to study the motion of a body of variable mass such as a rocket. The fundamental equation of motion of a body of variable mass is:
F = (v - u) dm/dt + m dv/dt
If the motion happens along a straight line, the scalar equivalent of the above equation is:
F = (v - u) dm/dt + m dv/dt
While other symbols have their usual meanings, dm/dt stands for rate of change in mass with time and dv/dt stands for rate of change in velocity with time. Some examples worth studying are a leaking sand-filled wagon on a frictionless track, sand pouring onto a conveyor belt and, of course, motion of a rocket.
Before we state the principle of conservation of linear momentum, a few terms need to be defined. A system is a well-defined collection of particles under investigation. All other particles in the universe except the system compose the surroundings.
Consider two interacting particles 1 and 2. The force exerted by 1 on 2 is F21 and that exerted by 2 on 1 is F12. If the system consists of only 1, 2 forms part of the surroundings and F12 is an external force on the system. Now, let us redefine the system such that it consists of both 1 and 2. In that case, both F21 and F12 have their sources within the system and are called internal forces. A system on which no net external force acts is called an isolated system.
The principle of conservation of linear momentum states that the total linear momentum of an isolated system remains constant. For a two-particle system, the mathematical statement of the principle would be:
m1 u1 + m2 u2 = m1 v1 + m2 v2
The symbols have their usual meanings.
Collision is defined as an event in which two (or more) particles come together for a short time and exert relatively large forces on each other to produce an abrupt change in motion of at least one of them. It usually implies a physical contact between colliding particles such as two billiard balls. However, this is not an essential condition. An alpha particle (He++) directed towards a gold nucleus deviates sharply from its original path even before any physical contact. Yet they are said to have "collided" because of the strong, brief electrostatic force of repulsion between them.
The coefficient of restitution, e, of a collision is a measure of the restitution (tendency to return to original shape) of the involved particles. It is given by the ratio of the velocity of separation after the collision to the velocity of approach before the collision. For a perfectly elastic collision, e = 1. For a perfectly inelastic collision, e = 0. For a partly elastic collision, 0 < e < 1. Most real collisions belong to this last category.
The centre of mass of a system of particles is defined as a point where the whole mass of the system may
be assumed to be concentrated such that the point would move in the same way as a single particle subjected to the
same external force would move.
Let us consider a system of n particles. The masses of the particles are m1, m2, …, mn.
Therefore, the total mass of the system of particles is M = m1 + m2 + … + mn.
At a given instant, the position coordinates of the particles in space are
(x1, y1, z1),
(x2, y2, z2), .... (xn, yn, zn).
At the same instant, the position coordinates of the centre of mass of the system will be:
xcm = (m1x1 + m2x2 + … + mnxn) / M
ycm = (m1y1 + m2y2 + … + mnyn) / M
Zcm = (m1z1 + m2z2 + … + mnzn) / M
For uniform rigid bodies of simple shape, the centre of mass can be located by inspection alone. For example, the centre of mass of a uniform rod coincides with its mid-point. The centre of mass of a uniform disc coincides with its geometric centre. The centre of mass of a uniform triangular plate coincides with its centroid, which is the intersection of the three medians.
For nonuniform rigid bodies or for uniform rigid bodies of not-so-simple shape, the centre of mass can be located by the method of integration. Examples of interest are nonuniform rod, uniform semicircular wire, semicircular plate, solid hemisphere etc, as we shall see in due course.
There are many instances of rotation around us. As a rotating body moves from one position to another, a straight line joining any two points on the body makes an angle with its previous position. This is an important criterion which helps to distinguish between rotation and certain kinds of curvilinear motion. In the first part, we discuss rotation about a fixed axis, otherwise known as pure rotation. The motion of a fan blade, a gramophone record, the steering wheel of a car etc is of this type. The second part deals with rotation about a moving axis which, in effect, is a combination of translation and rotation. A sphere rolling on the floor or a yo-yo bouncing up and down performs this kind of motion.
When a rigid body performs pure rotation, one line in the body (or body extended) remains fixed in space while all points not lying on the line move in circles, each having its centre on the fixed line. We call this line the axis of rotation. Because of this close connection between circular motion and rotational motion, the kinematic equations of circular motion developed earlier are also valid for rotation of a rigid body. As you will recall, the equations involve quantities such as angular displacement, angular velocity and angular acceleration.
The rotational effect of a force depends not only on its magnitude, but also on the position of its line of action. The effect is measured in terms of a physical quantity called torque or moment of a force. Suppose P is the position of a particle in the xy-plane. The line of action of the force F acting on the particle lies in the same plane. The position vector of P with respect to the origin O is r. Let the angle between the vectors r and F be θ. The torque τ of F about O is defined as the cross product of r and F. That is:
τ = r × F
The magnitude of the torque vector is given by:
τ = rF sinθ = Fd
where d = r sinθ is the perpendicular distance from O to the line of action of F.
The quantity d is known as the moment arm of F about O.
The direction of the torque follows from right-hand corkscrew rule. The dimensions of torque are
[ML2T-2] , and its SI unit is newton-metre (N-m).
Two equal and opposite forces having parallel lines of action form a couple. While the resultant of these two forces is zero, the net torque produced by them about any point is never zero.
The equation of rotational motion of a rigid body is:
τext = Iα
In the above expression, τext is the torque associated with external forces acting on the body, I is the moment of inertia of the body about the axis of rotation and α is its angular acceleration.
Recognize that this equation is the rotational analogue of F = ma, applied to the rectilinear motion of a particle.
A detailed study of moment of inertia will take us through the definition of radius of gyration and calculation of moment of inertia of various bodies by the method of integration. Two useful theorems on moment of inertia – parallel axes theorem and perpendicular axes theorem – will also be discussed.
Just like linear momentum is important in the discussion of translational motion, angular momentum
is important in the discussion of rotational motion. Consider a particle of mass m moving in the xy-plane. At some instant,
the particle is at the point P whose position vector with respect to the origin O is r. The velocity of the
particle at this instant is v, and therefore, its linear momentum is p = mv.
Let the angle between the vectors r and p be θ.
The angular momentum, l, of the particle about O is defined as the cross product of r and p. That is:
l = r × p
The magnitude of the angular momentum vector is given by:
l = rp sinθ = mvr sinθ
The direction of l is given, as usual, by the right-hand corkscrew rule.
According to the principle of conservation of angular momentum, the total angular momentum of a system of particles remains constant if the net external torque acting on the system is zero.
So far we discussed rotation of a rigid body about a fixed axis. We may now consider more general cases where the axis of rotation moves in space. Take the case of a wheel rolling on a horizontal straight road. An observer standing on the ground sees that the wheel rotates about a horizontal axis through the centre of mass and, at the same time, the centre of mass itself moves along a straight line. So this becomes a case of combined translational and rotational motion. A few cases worth analysing are rolling motion of a rigid body on horizontal floor and down an incline, a cylinder falling at the end of an unwinding string etc.
A body is said to have attained mechanical equilibrium if it either remains at rest or moves with a constant velocity. The branch of physics which studies the conditions of equilibrium of a body at rest is called statics. Strictly speaking, all bodies which attain equilibrium under a set of forces are deformed to a certain extent. However, for comparatively small forces, we may ignore the small deformations and treat the body under investigation as a perfectly rigid body.
Let us consider a three-dimensional rigid body of arbitrary shape in a frame of reference, Oxyz. A set of n external forces F1, F2, …, Fn are acting on the body. The static equilibrium of the rigid body requires the following conditions to be satisfied separately. The condition of translational equilibrium is:
∑ F = F1 + F2 + … + Fn = 0
If τ1, τ2, …, τn are the individual torques produced by the above forces about the origin O, the condition of rotational equilibrium is:
∑ τ = τ1 + τ2 + … + τn = 0
The torque equation is valid for any choice of origin inside or outside the boundaries of the body, provided the force equation holds good.
The number of velocity components required to completely describe the motion of a body is called the number of degrees of freedom of the body. An insect has one degree of freedom while walking along a straight wire, two degrees of freedom while crawling all over a flat table top, and a maximum of three degrees of freedom while flying randomly in the air. Treating the insect as a particle, all these degrees of freedom are associated with translational motion only. An extended body on the other hand is capable of both translation and rotation. Each type of motion contributes one to three degrees of freedom. In the most general case, an extended body acted upon by a set of non-coplanar forces has six degrees of freedom – three translational and three rotational. Now, each degree of freedom corresponds to one independent condition of equilibrium. In other words, the number of degrees of freedom is equal to the number of conditions of static equilibrium of a rigid body. Our video lectures mostly deal with simple cases involving coplanar forces and few equations, such as the equilibrium of a leaning ladder.
A statically indeterminate problem is one in which the number of unknown quantities is higher than the number of independent equations of equilibrium involving those unknowns. Obviously, such a problem cannot be solved. This type of situation arises when a body gets one or more extra support(s) over and above the minimum required for its equilibrium. An interesting example is a ladder resting on a rough floor against a rough wall.
The centre of gravity of a body is a fixed point through which the resultant of the forces of gravity acting on the constituent particles of the body passes, regardless of how the body is oriented in space. The centre of gravity and the centre of mass of a body are located at the same point, provided the body is placed in a uniform gravitational field. For exceptionally large bodies, such as a mountain, these two points do not coincide.
The stability of static equilibrium of a body can be determined as follows. Let the body be slightly tilted from its position of equilibrium. If a restoring torque comes into play and brings the body back to its initial position, the equilibrium is stable. If a destabilising torque comes into play and pushes the body further from its initial position, the equilibrium is unstable.
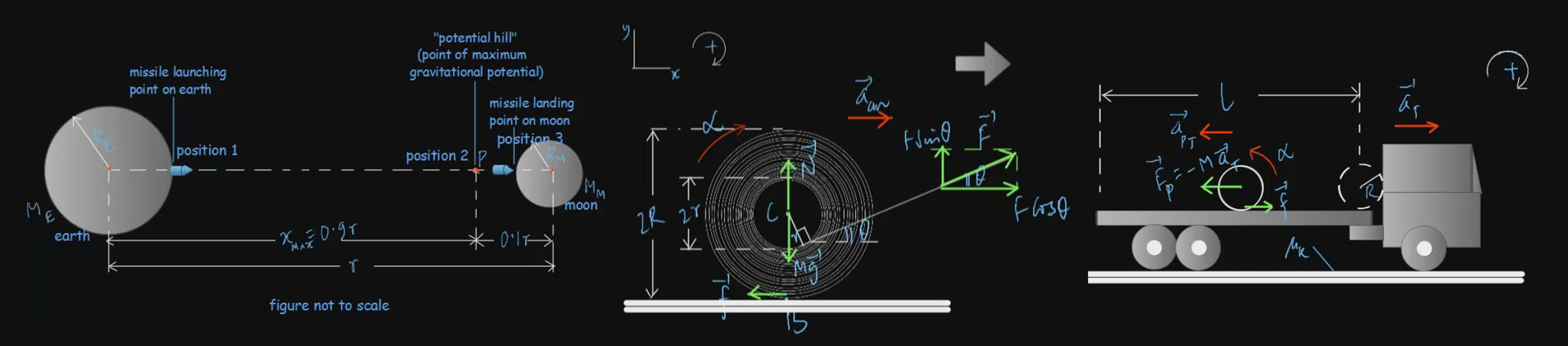
Newton's Law of gravitation states that every particle in the universe attracts every other particle with a force which is directly proportional to the mass of each particle and inversely proportional to the square of the distance between them. If two particles 1 and 2 have masses m1 and m2, and, the distance between them is r, the magnitude of the gravitational force between them is:
Fg = Gm1m2 /r2
The constant of proportionality G is called universal gravitational constant, and its value is 6.67 × 10-11 N-m2/ kg2.
Force of gravity is the special name given to the gravitational force exerted by the earth on any body on or near its surface. This force produces an acceleration due to gravity, g, in the body. The vector g is always directed towards the centre of the earth and its standard value at sea level at 45° latitude is 9.81 m/s2 . Variation of acceleration due to gravity happens due to a number of factors such as altitude, depth, earth's rotation and its non-spherical shape.
A body possesses two types of mass: inertial mass and gravitational mass. The concept of inertial mass comes from Newton's second law of motion. It gives a measure of resistance to any change of state of rest or motion under an external force. The concept of gravitational mass arises from Newton's Law of gravitation. It gives a measure of the force experienced by the body in a given gravitational field. Experiment shows inertial mass and gravitational mass of a body are the same.
Kepler's laws of planetary motion, as published by Johannes Kepler between 1609 and 1619, are as follows:
The gravitational field at a point in space is the gravitational force experienced by a unit mass placed at that point. The dimensions of gravitational field are [LT-2], and its SI unit is newton per kilogram (N/kg).
The gravitational potential energy of a system comprising two particles of masses m1 and m2 separated by distance r is:
U = - G m1m2 / r
This is a negative quantity, which becomes zero if the particles are at infinite separation.
The gravitational potential at a point due to a particle is the gravitational potential energy of a system comprising the particle in question and a unit mass placed at the given point. The dimensions of gravitational potential are [L2T-2], and its SI unit is joule per kilogram (J/kg).
The minimum speed with which a particle must be projected so that it may escape the gravitational attraction of the earth is called the escape speed for the earth. It is given by the formula:
vesc = √(2GME /RE)
where ME and RE are the mass and radius of the earth respectively. Its value is 11.2 km/s, independent of the angle of projection of the particle. Other heavenly bodies such as the sun, other planets and their moons also have their respective escape speeds. Escape speed assigned with a specific direction is called escape velocity.
Just like the planets revolve round the sun, many of the planets have one or more natural satellites revolving round them. A natural satellite is also called a "moon". The earth's moon is its only natural satellite. However, man has launched many artificial satellites in orbits round the earth. The orbital speed of a satellite in a circular orbit round the earth is given by:
vorb = √(GME / r)
Here r = RE + h is the orbit radius, h being the height of orbit above earth's surface. Orbital velocity at a given point on the orbit has magnitude equal to orbital speed and direction along the tangent to the orbit at the given point.
A geostationary satellite is an artificial satellite which always remains above the same spot on the equator. Its orbit is called geosynchronous orbit or parking orbit.
The total mechanical energy of satellite-earth system is given by:
E = - GME m / 2r
where ME is earth's mass, m is satellite's mass, and r is orbit radius.
Since a satellite revolving round the earth is in a state of free fall, the satellite and its occupants must also be weightless. An astronaut, like any other human, feels comfortable with the sensation of weight. Therefore, weightlessness of an astronaut during their long stay in an orbiting satellite is an unpleasant feeling and may cause medical symptoms.
The property by virtue of which a body resists any change in its size, shape or both and tends to regain its configuration on withdrawal of the deforming forces is known as the elasticity of the body.
If different parts of a body do not change their positions with respect to each other under the action of a system of balanced forces or couples, however large they may be, the body is called a perfectly rigid body. Glass is a good approximation to that. A perfectly elastic body completely regains its original configuration once the deforming forces are withdrawn. A quartz fibre is almost perfectly elastic. A perfectly inelastic body or plastic body does not show any tendency to recover its original configuration even after removal of the deforming forces. Putty is a close example.
The average stress, σ, across any given cross section of a body is defined as the ratio of the resultant internal force acting on the section to the area of that section. Thus, if the resultant internal force is F and the area of the cross section is A then:
σ = F / A
Suppose we resolve F into a component vector Fn normal to the section and a component vector Ft tangent to the section. Normal stress is defined as:
σn = Fn / A
Tangential stress or shear stress is defined as:
σt = Ft / A
The dimensions of stress are [ML-1T-2], and its SI unit is newton per square metre (N/m2).
Suppose two equal and opposite forces, F and - F, are applied to the ends of a solid rod of uniform cross section. If the forces act normally outward, the rod is said to be under tension. The stress at every perpendicular section of the rod is a normal tensile stress. On the other hand, if the forces act normally inward, the rod is under compression and the corresponding stress is a normal compressive stress. Both types of stress are known as longitudinal stress, because they act along the length of the rod.
A solid rectangular block, which attains static equilibrium under two pairs of forces applied tangentially to opposite faces, experiences shear stress. The same block, taken to a depth under the sea, experiences hydrostatic pressure of water acting normally inward on each of its six faces. The corresponding stress is called volume stress.
The strain of a body is the fractional change in its length, volume or shape relative to that in its original configuration. The ratio of two similar quantities, strain is a dimensionless number without units. As stress is the cause and strain is its effect, it is possible to relate each type of stress to a corresponding type of strain. Thus, longitudinal stress gives rise to longitudinal strain – either tensile strain or compressive strain, shear stress produces shear strain, and volume stress causes volume strain.
The fundamental law of elasticity is the Hooke's law which states that: "Provided the strain is small, the stress is proportional to the strain". The law implies that, within proportional limit, the ratio of stress to strain is a constant known as the elastic modulus of the material. The dimensions of elastic modulus are [ML-1T-2], and its unit is N/m2.
In accordance with three types of stress and strain mentioned above, three types of elastic modulus can be defined. Young's modulus is the ratio of longitudinal stress to longitudinal strain. Shear modulus is the ratio of shear stress to shear strain. Bulk modulus is the ratio of volume stress to volume strain. While only a solid can have Young's modulus and shear modulus, bulk modulus is a characteristic of solids, liquids and gases.
Another elastic constant of importance is Poisson's ratio. A longitudinal strain produced in a rod is always accompanied by a lateral strain produced simultaneously. The negative of the ratio of lateral strain to longitudinal strain is known as Poisson's ratio for the material of the rod. The relations among elastic constants will be discussed in due course.
Although the relation between stress and strain follows Hooke's law for small strains, it becomes complex if the strain is large. Therefore, it is instructive to plot a stress versus strain graph for a typical ductile metal wire. There are certain terms of interest regarding this graph, such as proportional limit, elastic limit or yield point, breaking stress, necking, breaking point, crushing point etc. The lack of coincidence between the curves for increasing and decreasing stress is known as elastic hysteresis.
The elastic potential energy stored in a wire stretched within proportional limit is given by the formula:
U = YA(∆l)2 / 2l
where Y is the Young's modulus, A is the cross-sectional area, ∆l is the extension and l is the original length of the wire. Another useful formula for elastic potential energy stored per unit volume, or energy density, is:
Energy density = 1/2 × stress × strain
This last relationship is valid also if the body is under shear stress or volume stress.
Matter can be classified into three types: solids, liquids and gases. A solid can withstand shear stress; it has definite volume and shape. Liquids and gases cannot withstand static shear stress and begin to flow under it; hence they are collectively referred to as fluids. None of the fluids has any definite shape of its own and eventually takes the shape of the vessel in which it is kept. While a liquid occupies a definite volume almost unaffected even by very high pressure, a gas can be compressed easily.
The mechanics of fluids is governed by a number of physical principles, which are based on Newton's laws of motion and other force laws. Our present topic of discussion is fluids at rest, or fluid statics. Later we shall deal with fluids in motion, or fluid dynamics. Two important fluid properties, surface tension and viscosity, will be introduced in between for a comprehensive understanding of fluid mechanics as a whole.
The density, ρ, of a homogenous substance is its mass per unit volume. If m is the mass of a substance of volume V, its density is:
ρ = m / V
The dimensions of density are [ML-3], and its SI unit is kilogram per cubic metre (kg/m3). The relative density or specific gravity of a substance is the ratio of its density to the density of water at 4°C and 1 atm pressure.
The hydrostatic pressure, P, at any point inside a fluid at rest is defined as the magnitude of the normal force exerted by the fluid on unit area containing the point. If the pressure is the same at all points of a finite plane surface of area A, we may write:
P = F / A
where F is the normal force acting on the area. This force is called thrust. The dimensions of pressure are [ML-1T-2], and its SI unit is N/m2 or pascal (Pa). The standard atmospheric pressure is taken to be 1.013 × 105 N/m2. Although in most cases absolute pressure is quoted, in case of car tyres and human heart gauge pressure is quoted which is the pressure in excess of normal atmospheric pressure.
The absolute pressure at a depth h below the surface of a liquid open to the atmosphere is:
P = Pa + ρgh
where Pa is the atmospheric pressure, ρ is the density of the liquid and g is acceleration due to gravity. This last equation has an interesting implication. If water is poured up to the same height in a number of vessels of different shapes but equal bottom areas, the thrusts on the bottom of all vessels will be equal regardless of different quantities of water in them! This phenomenon is called hydrostatic paradox. Note further that, if the vessel is accelerated, the above formula will not hold. Two special cases of interest are vessel moving with constant linear acceleration and vessel rotating about a vertical axis with constant angular velocity.
A mercury barometer is used to measure atmospheric pressure. A manometer is used to measure gauge pressure at a certain point in a fluid.
Pascal's principle states that the pressure applied to an enclosed liquid is transmitted undiminished to every point of the liquid and to the walls of the container. The principle has widespread applications in the design of hydraulic press, hydraulic jack, remote control etc.
The upward force exerted by a fluid on a body partially or totally immersed in it is called the buoyant force. The effect is known as buoyancy. The magnitude of buoyant force was first determined by Greek scientist Archimedes (287-212 BC). Archimedes' principle states that:
The buoyant force on an immersed body has the same magnitude as the weight of the fluid displaced by the body.
The buoyant force acts vertically upward through the centre of buoyancy which coincides with the centre of gravity of the displaced fluid before its displacement.
Next we examine the conditions of immersion and flotation. A body, which is either completely immersed in a fluid or floats on its surface, experiences two vertical forces: force of gravity, Fg , and buoyant force, FB . The densities of the body and the fluid are assumed ρ and ρf respectively. Suppose the body is taken below the surface of the fluid and released there. If ρ > ρf then Fg > FB, and the body sinks to the bottom of the vessel. If ρ < ρf then Fg < FB , and the body rises towards the surface of the fluid. If ρ = ρf then Fg = FB , and the body remains at rest exactly where it is released without sinking or rising.
When a body floats on a fluid, it is only partially immersed in it. The fraction of the total volume of a floating body which remains immersed inside a fluid is equal to the ratio of the density of the body to the density of the fluid. A beautiful example of flotation is a cartesian diver, an ingenious toy invented by René Descartes.
Surface tension is an important fluid property which can explain events like a piece of camphor dancing on the surface of water, a water spider skating on a pond without wetting its legs, a needle floating on water, and so on. It is a molecular phenomenon which occurs at the surface of separation between two phases, such as a liquid in contact with air.
We begin with some important definitions. The force of attraction between the molecules of two different substances is known as the force of adhesion or adhesive force. The force of attraction between the molecules of the same substance is known as the force of cohesion or cohesive force. The molecular range of a substance is the maximum distance between its two molecules up to which the cohesive force is effective. If a plane is imagined within the liquid parallel to its free surface at a distance equalling the molecular range, the portion of the liquid lying between the free surface and the plane is known as the surface film.
All molecules lying in the surface film of a liquid experience a net inward force. Every time an external agent wants to increase the area of the free surface of a liquid, it must do so by raising molecules from the bulk of the liquid to the surface against the said inward force. The work done by the external agent is stored as potential energy in the free surface and known as free surface energy. Thus, the larger the surface area of a liquid, the more free surface energy it possesses. Since stable equilibrium is attained at minimum potential energy, the liquid surface behaves like a stretched elastic skin always trying to contract in area.
The force of surface tension, or simply surface tension, is defined as the tensile force acting across and perpendicular to a short, straight line on the surface of liquid divided by the length of that line. The dimensions of surface tension are [MT-2], and its SI unit is newton per metre (N/m). It can be shown that, in general, the surface tension of a liquid is equal to its free surface energy per unit surface area.
When a liquid comes into contact with a solid wall, the liquid surface near the point of contact is usually curved. The angle between the tangent to the liquid surface at the point of contact and the solid surface measured from within the liquid is known as the angle of contact for that pair of liquid and solid. This angle of contact may be an acute angle (< 90°) as in the case of methylene iodide and glass, an obtuse angle (> 90°) as in the case of mercury and glass, or a right angle ( = 90°) as in the case of water and silver.
The curved liquid surface near a solid wall is known as a meniscus. The possible shapes of a meniscus can be explained on the basis of the intermolecular forces of adhesion and cohesion. A typical liquid molecule on the meniscus experiences adhesive forces exerted by the solid molecules, cohesive forces exerted by other molecules of the liquid, and the force of gravity which is comparatively small. Thus, the relative strengths of adhesive and cohesive forces determine whether the meniscus would be concave, convex or flat.
The excess pressure within a liquid drop is given by the formula:
P - Pa = 2γ / R
where P is the pressure inside the liquid drop of radius R, Pa is atmospheric pressure and γ is the surface tension of the liquid.
The excess pressure within a soap bubble is given by the formula:
P - Pa = 4γ / R
where the symbols have similar meanings as before. When we derive these two important formulas, we shall see why a multiplication factor of 2 is coming in the case of a soap bubble. More rigorous calculation will be required to determine the force between two plates separated by a liquid film such as water or mercury.
An important effect of surface tension is the rise or fall of a liquid in a capillary tube. An open tube of very small cross section is known as a capillary tube, and the said effect is called capillarity. If the angle of contact between the liquid and the material of the tube is less than 90°, as in the case of water and glass, the liquid rises in the tube. Conversely, if the angle is greater than 90° as with mercury and glass, the liquid level falls in the tube. The common formula for the rise or fall, as the case may be, is:
h = 2γ cosφ / rρg
In this expression, h is the elevation or depression, γ and ρ are the surface tension and density of the liquid respectively, φ is the angle of contact, r is tube radius, g is acceleration due to gravity. The inverse relation between h and r is sometimes referred to as Jurin's law. The rise of ink through the pores of a blotting paper or of oil through the wick of a lamp is an example of capillary action.
The factors affecting surface tension are contamination of the liquid surface, presence of dissolved substances, variation in temperature, and nature of medium in contact.
Fluid dynamics is the study of fluids in motion. Since the motion of a real fluid is complex, the treatment is simplified by making a few assumptions. We consider an ideal fluid which is non-viscous and incompressible. The flow of the ideal fluid is assumed to be steady and irrotational. Steady flow means the velocity of the fluid at a given point remains constant in time, and variation in velocity from point to point must be smooth.
The path followed by a fluid element under steady flow is called a streamline. The line can either be straight or curved such that the tangent drawn to it at any point gives the direction of flow of the fluid at that point. Steady flow is also called streamline flow or laminar flow. Example is water flowing through a tube at low speed.
On the other hand, if the fluid moves at high speed or the bounding surfaces cause abrupt changes in its velocity, the flow becomes irregular and complex. Such a flow is called a turbulent flow. Example is flow of water in a stream near boulders.
According to equation of continuity, the product of the cross-sectional area and the speed of an ideal fluid in steady flow remains constant at all points along a tube. The equation is based on the assumption that no fluid can flow across the wall of the tube, and there is no "source" or "sink" inside the tube which can create or destroy any fluid.
When a fluid flows steadily through a pipe of varying cross section and elevation, the pressure within the pipe changes along its length. The way the pressure depends on the fluid's speed and the pipe's elevation is governed by Bernoulli's principle. One way of writing Bernoulli's equation is:
P + 1/2 ρv2 + ρgy = constant
Put in words, the sum total of the pressure, kinetic energy per unit volume and gravitational potential energy per unit volume of an ideal fluid in steady flow remains constant along a streamline.
There are interesting applications of Bernoulli's equation. One of them is to determine the speed of efflux, that is the speed with which a liquid emerges from a hole made at the wall of its container. Venturi tube is a horizontal constricted pipe used to measure the flow speed of an incompressible fluid. Pitot tube is another device to measure fluid speed. The ascent of an aeroplane is made possible by a net upward force — known as dynamic lift — on its wings. The shape and orientation of the wing are designed such that the speed of air is greater above the wing and hence, by Bernoulli's principle, air pressure is higher under the wing.
Unlike ideal fluids, a real fluid possesses a property called viscosity. When a real fluid flows through a pipe, the velocity of the fluid layer gradually increases from zero at the pipe wall to a maximum at the centre. The force of internal friction between the layers is known as viscous force. Newton's formula applicable to laminar flow of a viscous fluid is:
Ft = η A dv/dy
where Ft is the tangential force acting on fluid surface of area A, dv/dy is speed gradient, and η is coefficient of viscosity of the given fluid. The dimensions of viscosity coefficient are [ML-1T-1], and its unit is newton second per square metre (N-s/m2).
Poiseuille's law on laminar viscous flow in a pipe is:
φ = πΔP R4 / 8ηl
In this expression, φ is volume flux (in m3/s), ΔP is pressure difference between two ends of the pipe of length l and radis R, η is coefficient of viscosity of the fluid.
The minimum speed of a fluid in a pipe above which the fluid ceases to be steady is called the critical speed of the fluid. Reynolds number, NR , suggests whether the flow of a viscous fluid in a pipe would be steady or turbulent. Experiments show that if NR does not exceed 2000, the flow is steady; if NR exceeds 3000, the flow is turbulent; if NR falls between 2000 and 3000, the flow may be either steady or turbulent depending on the shape of the pipe entrance and the distance from it.
When a solid body moves through a viscous fluid, it experiences a resistive drag force exerted by the fluid on it. For a slow-moving spherical body, this drag force is given by Stoke's law as follows:
FD = 6πηrv
On the right-hand side, η is the coefficient of viscosity of the fluid and r is the radius of the body moving with speed v relative to the fluid. Under the combined effects of this drag force, force of gravity and force of buoyancy, the sphere eventually falls with a constant terminal speed.
In general, all bodies expand when they are heated and contract when cooled. The expansion or contraction, as the case may be, is small in solids, larger in liquids, and the largest in gases. The increase in length, width or height of a solid is called linear expansion. The increase in area is called surface expansion. The increase in volume is called volume expansion or cubical expansion. A liquid or a gas has only volume expansion.
Suppose the length of a rod increases from an initial value of l1 at temperature θ1 to a final value of l2 at higher temperature θ2. The relation between these two lengths is:
l2 = l1 [1 + α (θ2 - θ1)]
Here α is a constant of proportionality, known as the coefficient of linear expansion for the solid material of the rod. The dimension of α is [K-1] , and its unit is per kelvin (/K).
In a similar way, we can relate the surface areas of a solid plate at two different temperatures as:
S2 = S1 [1 + β (θ2 - θ1)]
where β is the coefficient of surface expansion for the solid. And for change in volume with temperature:
V2 = V1 [1 + γ(θ2 - θ1)]
The quantity, γ, is the coefficient of volume expansion. All these three coefficients have the same dimension and the same unit. And for an isotropic solid, a simple relation exists among them:
α = β/2 = γ/3
Thus, referring to one table for the values of α of various solids, we can determine the corresponding values of β and γ.
Some notable effects of thermal expansion of solids are expansion of a measuring scale, a faulty pendulum clock that runs slow in summer, thermal stress experienced by a rod fixed between two rigid walls, deformation of a bimetallic strip that is cleverly used in a thermostat to switch an air-conditioner on and off.
While discussing the expansion of liquids, it must be kept in mind that both the liquid and the solid container expand in volume as temperature goes up. So it is important to distinguish between apparent expansion and real expansion of a liquid. Correspondingly, there would be two coefficients for a liquid: coefficient of apparent expansion and coefficient of real expansion. The relation between these two coefficients is:
γr = γa + γg
The symbols are nearly self-explanatory; γg is the coefficient of volume expansion of glass or any other solid material from which the container is made. The coefficients of real expansion of liquids are significantly greater than the coefficients of volume expansion of solids.
Some devices to measure the coefficients of expansion of a liquid are dilatometer or volume thermometer, weight thermometer, Dulong and Petit's apparatus etc.
One notable effect of thermal expansion of liquids is the change in buoyant force on an immersed body with change in temperature. Another is the correction factor to be introduced to the reading of a barometer if the ambient temperature is different from the temperature of calibration. Anomalous expansion of water refers to the strange phenomenon of water contracting in volume as its temperature rises from 0°C to 4°C, implying a negative expansion coefficient in that range!
Expansion of gases is dictated by three famous laws: Boyle's law, Charles' law and pressure law. The last two laws lead us to the concept of absolute zero of temperature, which is - 273.15°C or 0 K. This is the temperature at which, theoretically, a gas would occupy zero volume and exert zero pressure. In reality, all gases change into liquid phase much above absolute zero. Combining Boyle's law and Charles' law, we can arrive at the equation of state of an ideal gas which is:
PV = nRT
Here P is pressure and V is volume of n moles of gas at Kelvin temperature T. The quantity R is called universal gas constant, because its value is the same 8.31 J/mol-K for all gases. The ratio of universal gas constant and Avogadro's number is called Boltzmann's constant. The equation of state of a gas mixture can be derived by making use of Dalton's law of partial pressure.
Heat is defined as the thermal energy that flows from a system to its surroundings or the other way round solely as a result of the difference between their temperatures. The flow always takes place from a higher temperature to a lower temperature, and never in the reverse direction. The CGS unit of heat is calorie (cal); a larger unit kilocalorie is also used. Since heat is now recognised as a form of energy, CGPM insists that we use the SI unit of energy, joule (J), as the unit of heat. 1 cal = 4.186 J.
The specific heat capacity, or simply specific heat, of a substance is defined as the amount of heat required to raise the temperature of unit mass by one degree. Its SI unit is J/kg-K. If Q is the heat supplied to raise temperature of a body of mass m and specific heat capacity c from θ1 to θ2 then:
Q = cm (θ2 - θ1)
The molar heat capacity or molar specific heat of a substance is defined as the amount of heat required to raise the temperature of one mole of the substance by one degree. Its SI unit is J/mol-K. If Q is the heat required to raise temperature of n moles of a substance of molar heat capacity C from θ1 to θ2 then:
Q = Cn (θ2 - θ1)
The heat capacity of a body is defined as the amount of heat required to raise its temperature by one degree. Its SI unit is J/K. Once you distinguish heat capacity from molar heat capacity and specific heat capacity, you should be able to deduce the relation between any two of them.
The water equivalent of a body is the mass of water which has the same heat capacity as the body itself.
When a hot body is brought into contact with comparatively cold surroundings, heat flows from the body to the surroundings until their temperatures become equal. The experiments of calorimetry are usually carried out inside a properly insulated metal vessel known as a calorimeter. The hot body placed in the vessel is the "system"; the calorimeter and calorimetric liquid together are the "surroundings". Assuming no heat enters or exits the calorimeter and no chemical reaction takes place inside it:
Heat lost by hotter system = heat gained by colder surroundings
This is the fundamental principle of calorimetry.
The term phase means the state in which a substance exists, i.e. solid, liquid or gas. For example, the chemical substance H2O exists as ice in the solid phase, water in the liquid phase and water vapour or steam in the gas phase.
When a substance changes phase, the process does not take place abruptly. It happens at a constant temperature, even though heat is either supplied to or withdrawn from the system. The amount of heat required to change the phase of unit mass of a substance is known as the latent heat, L, of the substance. If Q is the amount of heat required to change the phase of mass m of a substance then:
Q = mL
The SI unit of latent heat is J/kg. If the phase changes from solid to liquid, we use the term latent heat of fusion. If the change happens from liquid to gas, the term used is latent heat of vaporisation. There are standard calorimetric experiments to determine latent heat of fusion of ice and latent heat of vaporisation of water. The first one is 3.33 x 105 J/kg, while the latter is 2.26 x 106 J/kg.
The equivalence between mechanical work and heat was established in the 19th century chiefly through the efforts of Robert Mayer and Helmholtz in Germany and James Joule in England. If W is the mechanical work which produces the same rise in temperature of a system as does the flow of heat Q then:
W = JQ
The quantity J is a constant of proportionality known as the mechanical equivalent of heat. The best modern value of J is 4.186 J/cal.
Let us touch upon various types of phase change. The change of phase from solid to liquid is called fusion or melting. The reverse process in which a substance changes from liquid to solid phase is called freezing or solidification. The temperature at which melting takes place under a pressure of 1 atm is called the normal melting point of the substance. The temperature at which freezing takes place under 1 atm pressure is called the normal freezing point of the substance. For a crystalline substance, these two temperatures are usually the same.
The change of phase from liquid to vapour is called vaporisation. The reverse process in which a substance changes from vapour to liquid is called condensation. Vaporisation can take place in two ways: evaporation and boiling. Evaporation is a slow process which happens at any temperature from the surface of a liquid. Shallow ponds dry up in summer due to evaporation. Boiling is a rapid, vigourous process that takes place throughout the mass of the liquid. The temperature at which boiling takes place under a pressure of 1 atm is called the normal boiling point of the substance.
Substances like iodine, camphor and naphthalene change directly from solid to vapour phase on heating. This type of phase change is called sublimation. The amount of heat absorbed by unit mass of a substance to sublimate is called the latent heat of sublimation.
The experiments of James Joule during the 1840s proved beyond doubt that mechanical work and heat are equivalent. They also delivered the final blow to the erstwhile caloric theory of heat. The collapse of caloric theory inspired three gentlemen — Rudolf Clausius, Clerk Maxwell and Ludwig Boltzmann — to develop the kinetic theory of gases from a theoretical standpoint. The experimental proof of kinetic theory came a few decades later, in 1909, chiefly through the investigation of Brownian motion by Albert Einstein and Jean Perrin. Although originally developed for gases, kinetic theory can be extended to explain the thermal phenomena in solids and liquids.
The total energy of a system usually consists of external energy and internal energy. External energy is made up of potential energy due to an external conservative force and kinetic energy due to the motion of the system as a whole relative to its surroundings. Internal energy is made up of intermolecular potential energy, energy of molecular motion relative to the centre of mass of the system, and intramolecular energy. The energy of molecular motion (which can be translation, rotation and vibration) is the disordered part of internal energy and known as thermal energy. Even though it is impossible to determine how much internal energy a system possesses, we are interested only in the change in internal energy between two states and there are alternative methods to determine that.
The kinetic model of an ideal gas proposes a microscopic model in which any pure gas is made up of a large number of identical minute particles called "molecules". The molecules move randomly in the container in any direction at any speed between zero and infinity. As they move, molecules collide with one another and with the walls of the container. These collisions are all perfectly elastic and of negligible duration compared to the time spent between two successive collisions.
Using the kinetic model, the pressure exerted by an ideal gas is:
P = Mvrms2 / 3V = ρvrms2 / 3
where ρ is the density of the gas and vrms is the root mean square speed or RMS speed of the molecules of the gas. It follows that RMS speed can be expressed as:
vrms = √(3 RT / M0)
where M0 is the molar mass and T is the Kelvin temperature of the gas; R is the universal gas constant. Typically, the RMS speeds of hydrogen and oxygen gas molecules are 1836 m/s and 461 m/s respectively at 0°C.
It must be clearly understood that all molecules of a gas do not move with RMS speed. Many of the molecules move at speeds higher than RMS speed, while many others move at lower speeds. The distribution of molecular speeds is governed by a complex equation known as Maxwell distribution function. In fact, three different speeds are associated with Maxwell speed distribution curve. They are RMS speed, average speed and most probable speed. vrms > vav > vmp
The distance travelled by a molecule between two successive collisions is known as the free path and the average value of this quantity is called mean free path. The number of collisions taking place per unit time is called collision frequency. The reciprocal of collision frequency is called mean free time.
A gas which obeys the equation of state, PV = nRT, in all circumstances is known as an ideal gas. Strictly speaking, no real gas obeys the equation of state. But helium, hydrogen, nitrogen and oxygen which have extremely low boiling points behave like an ideal gas at room temperature and low pressure. Among several modified equations proposed for real gases, the best known is van der Waals' equation:
(P + n2a /V2)(V - nb) = nRT
In the expression, P, V and T have usual meanings; n is number of moles of the gas; a and b are positive constants characteristic of the gas.
When a space contains the maximum amount of vapour it can hold at a given temperature, the vapour is said to be saturated vapour. A vapour whose concentration is less than the maximum possible is said to be unsaturated vapour. The saturation vapour pressure (s.v.p. in short) of a liquid is the maximum pressure exerted by its vapour at a given temperature. In this context, two types of phase diagram are discussed: pressure-temperature phase diagram and pressure-volume phase diagram. Terms such as critical point and triple point are also introduced.
Because of continuous evaporation from the seas, rivers, moist earth etc, the atmosphere always contains varying amounts of water vapour. Hygrometry deals with the measurement of the amount of water vapour in a given volume of air. If air is gradually cooled to a temperature at which the s.v.p. of water is just equal to the actual pressure of water vapour, that temperature is called the dew point. If the temperature of air falls below the dew point, some vapour condenses and appears as tiny drops of water, which we call dew. The dew point varies with location and time.
The absolute humidity is defined as the mass of water vapour present per unit volume of air. A more useful term is relative humidity, which is the ratio of the mass of water vapour present in a given volume of air to the mass of water vapour required to saturate the volume. Regnault's hygrometer is a useful device to measure the relative humidity of air.
Thermodynamics is the branch of science which deals with the interconversion of heat and mechanical work, and the change in the properties of a system as it gains or loses energy in either form. Thermodynamics is mainly based on two empirical laws. Two system properties — internal energy and enthalpy — are associated with the first law. Another property called entropy is established as a consequence of the second law.
If a system is such that only heat can flow and work can be performed across its boundary but no matter can pass across, the system is called a thermodynamic system. The surroundings of a thermodynamic system are all other systems with which it can exchange energy. The thermodynamic properties are those characteristics of a system which describe its state. Thus, for a given amount of the gas, temperature (T), volume (V) and pressure (P) are its three thermodynamic properties. When a system simultaneously satisfies all the conditions necessary for thermal, mechanical and chemical equilibrium, no change is observed in the thermodynamic properties with time and the system is said to be in thermodynamic equilibrium. The path comprising a series of states through which the system passes to move from the initial state to the final state is called a process. If a system goes through a number of processes to eventually return to its initial state, we say that the system has gone through a cycle.
The Clausius statement of the first law of thermodynamics is:
The total energy of an isolated system remains constant whatever changes may occur within it. In mathematical terms:
Q = Δ U + W
where Q is the heat given to or withdrawn from the system, W is the work done by or on the system and ΔU is the change in internal energy of the system. All these three quantities may have positive or negative values depending on different possibilities.
A quasi-static process is one in which the properties of a system change so slowly that the deviation from thermodynamic equilibrium is infinitesimal. That is, each intermediate state through which the system passes during the process may be approximated as an equilibrium state. A quasi-static process can be plotted on a P-V, T-V or T-P diagram, while a non-quasistatic process can't be plotted.
Among the different types of molar heat capacity of an ideal gas, the molar heat capacity at constant volume, CV, and the molar heat capacity at constant pressure, CP, are of practical use. If QV is the heat required to raise temperature of n moles of a gas through ΔT at constant volume then:
QV = nCV ΔT
Similarly, if QP is the heat required to raise temperature of n moles of a gas through ΔT at constant pressure then:
QP = nCP ΔT
The relationship between these two molar heat capacities is given by Mayer's equation, which is:
CP = CV + R
Heat capacity ratio, γ, is the ratio of molar heat capacities of an ideal gas. That is:
γ = CP/CV
Kinetic theory of gases correctly predicts that, for monatomic gases, CV = 3R /2, CP = 5R /2, γ = 1.67; for diatomic gases, CV = 5R /2, CP = 7R /2, γ = 1.40; for polyatomic gases, CV = 3R, CP = 4R, γ = 1.33.
There are various types of quasi-static thermodynamic process, depending on which quantity remains constant and which quantities vary during the process. In an isothermal process, temperature remains constant while pressure and volume vary. In an isochoric process, volume remains constant while temperature and pressure very. In an isobaric process, pressure remains constant while temperature and volume vary. In an adiabatic process, no heat flows in or out of the system while temperature, volume and pressure all vary. We shall derive important results for Q, Δ U and W for each of the processes mentioned above in due course.
The Kelvin-Planck statement of the second law of thermodynamics is:
It is impossible to remove thermal energy from a system at a single temperature and convert it into an equivalent amount of mechanical work without changing the system or the surroundings in some other way.
From an engineering point of view, the most important application of the second law is the limited efficiency of heat engines. A heat engine is a device which continuously converts thermal energy into mechanical work. The thermal efficiency of a heat engine is the ratio of the work done by the engine to the heat absorbed by it from the hot reservoir. Notable examples of heat engine are steam engine and internal combustion engine. There are two types of internal combustion engine: spark ignition engine such as a petrol engine and compression ignition engine such as a diesel engine. The diesel engine has the highest thermal efficiency.
A process which can advance only in forward direction is called an irreversible process. But if a process, operated backwards, takes the system through the same equilibrium states in the reverse order, the original process is known as a reversible process. If a process has to be reversible, it must be quasi-static, non-dissipative and any transfer of heat must take place isothermally. A heat engine cycle which consists only of reversible processes is called a reversible cycle, and the engine is called a reversible engine. In 1824, French physicist Sadi Carnot showed that a reversible engine is the most efficient of all heat engines. Such an engine is known as a Carnot engine, and the cycle followed by it is called Carnot cycle. The formal statement of Carnot theorem is:
No heat engine operating between two given heat reservoirs can be more efficient than a Carnot engine operating between the same two reservoirs.
Carnot efficiency, which is the thermal efficiency of a Carnot engine, is given by the formula:
ηC = 1 - Tc/Th
Here Tc and Th are the temperatures of the cold and hot reservoirs respectively. The result is independent of the working substance used in the engine!
When a heat engine is run in reverse, heat is transferred from the cold reservoir to the hot reservoir and work must be performed on the system. This is the mode of operation of a refrigerator or a heat pump. A Carnot engine run in reverse is called a Carnot refrigerator. Just like Carnot engine, a Carnot refrigerator has the highest coefficient of performance or COP operated between two fixed temperatures.
A common feature of all irreversible processes is that they take the system plus the surroundings towards greater disorder. The concept of entropy, S, was first introduced by Rudolf Clausius. It is an extensive thermodynamic property which gives the measure of a system's disorder. The unit of entropy is joule per kelvin (J/K).
We are confident of getting your support and appreciation. That will inspire us to add new features to our website, such as question & problem banks, doubt removal sessions etc. Please let me know your feedback
Hearty welcome to Physicsacademyonline.in / PhysicsAcademyOnline.com /PhysicsAcademyOnline.org / PhysicsAcademyOnline.info / PhysicsAcademyOnline.net.