
Matter can be classified into three types: solids, liquids and gases. A solid can withstand shear stress; it has definite volume and shape. Liquids and gases cannot withstand static shear stress and begin to flow under it; hence they are collectively referred to as fluids. None of the fluids has any definite shape of its own and eventually takes the shape of the vessel in which it is kept. While a liquid occupies a definite volume almost unaffected even by very high pressure, a gas can be compressed easily.
The mechanics of fluids is governed by a number of physical principles, which are based on Newton's laws of motion and other force laws. Our present topic of discussion is fluids at rest, or fluid statics. Later we shall deal with fluids in motion, or fluid dynamics. Two important fluid properties, surface tension and viscosity, will be introduced in between for a comprehensive understanding of fluid mechanics as a whole.
The density, ρ, of a homogenous substance is its mass per unit volume. If m is the mass of a substance of volume V, its density is:
ρ = m / V
The dimensions of density are [ML-3], and its SI unit is kilogram per cubic metre (kg/m3). The relative density or specific gravity of a substance is the ratio of its density to the density of water at 4°C and 1 atm pressure.
The hydrostatic pressure, P, at any point inside a fluid at rest is defined as the magnitude of the normal force exerted by the fluid on unit area containing the point. If the pressure is the same at all points of a finite plane surface of area A, we may write:
P = F / A
where F is the normal force acting on the area. This force is called thrust. The dimensions of pressure are [ML-1T-2], and its SI unit is N/m2 or pascal (Pa). The standard atmospheric pressure is taken to be 1.013 × 105 N/m2. Although in most cases absolute pressure is quoted, in case of car tyres and human heart gauge pressure is quoted which is the pressure in excess of normal atmospheric pressure.
The absolute pressure at a depth h below the surface of a liquid open to the atmosphere is:
P = Pa + ρgh
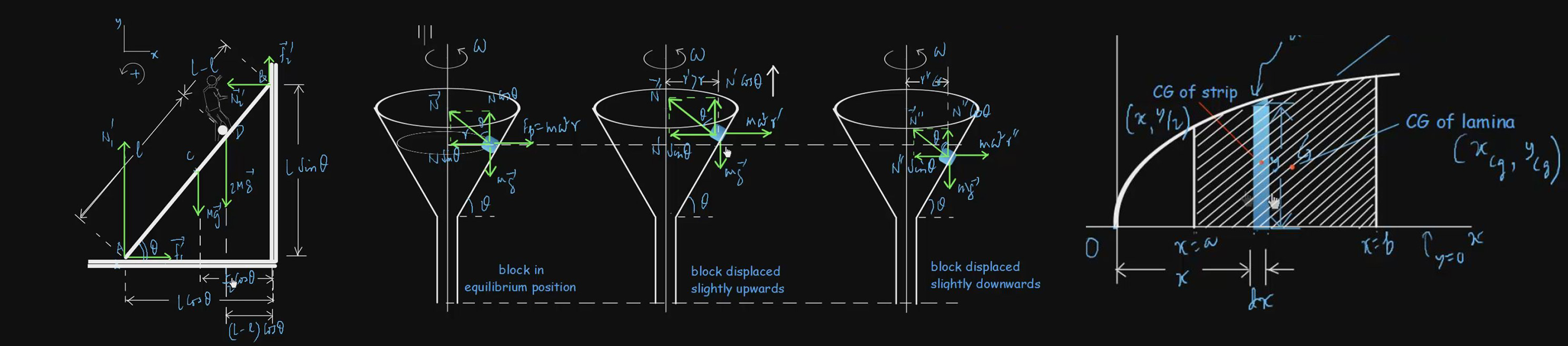
where Pa is the atmospheric pressure, ρ is the density of the liquid and g is acceleration due to gravity. This last equation has an interesting implication. If water is poured up to the same height in a number of vessels of different shapes but equal bottom areas, the thrusts on the bottom of all vessels will be equal regardless of different quantities of water in them! This phenomenon is called hydrostatic paradox. Note further that, if the vessel is accelerated, the above formula will not hold. Two special cases of interest are vessel moving with constant linear acceleration and vessel rotating about a vertical axis with constant angular velocity.
A mercury barometer is used to measure atmospheric pressure. A manometer is used to measure gauge pressure at a certain point in a fluid.
Pascal's principle states that the pressure applied to an enclosed liquid is transmitted undiminished to every point of the liquid and to the walls of the container. The principle has widespread applications in the design of hydraulic press, hydraulic jack, remote control etc.
The upward force exerted by a fluid on a body partially or totally immersed in it is called the buoyant force. The effect is known as buoyancy. The magnitude of buoyant force was first determined by Greek scientist Archimedes (287-212 BC). Archimedes' principle states that:
The buoyant force on an immersed body has the same magnitude as the weight of the fluid displaced by the body.
The buoyant force acts vertically upward through the centre of buoyancy which coincides with the centre of gravity of the displaced fluid before its displacement.
Next we examine the conditions of immersion and flotation. A body, which is either completely immersed in a fluid or floats on its surface, experiences two vertical forces: force of gravity, Fg , and buoyant force, FB . The densities of the body and the fluid are assumed ρ and ρf respectively. Suppose the body is taken below the surface of the fluid and released there. If ρ > ρf then Fg > FB, and the body sinks to the bottom of the vessel. If ρ < ρf then Fg < FB , and the body rises towards the surface of the fluid. If ρ = ρf then Fg = FB , and the body remains at rest exactly where it is released without sinking or rising.
When a body floats on a fluid, it is only partially immersed in it. The fraction of the total volume of a floating body which remains immersed inside a fluid is equal to the ratio of the density of the body to the density of the fluid. A beautiful example of flotation is a cartesian diver, an ingenious toy invented by René Descartes.